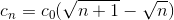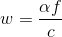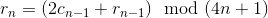The stepper motor is an electromagnetic device that converts digital pulses into mechanical shaft rotation.
Most common types of stepper motor can be bipolar or unipolar, depending on the winding.
To make a stepper motor move, motor windings must be loaded in the correct order.
A stepper motor move at steps, it's accuracy is usually expressed as degree per step. Microstepping is a method by witch motor accuracy can be increased at the expense of the motor torque.
Stepper motor can be driven using straight dual H-bridge driver. However there is a family of IC expressily built to drive stepper motor, they incorporate microstepping technique and are driven by a built-in translator, so that each received pulse is translated to a motor step.
Allegro MicroSystems offers a wide range of bipolar stepper motor driver.
This library drive a stepper motor using the Allegro A3967 (EasyDriver) on ATmega8. It will also work on the Allegro a4988, and other type of motor driver controlled by the number of pulse received.
It features:
- direction changing
- speed changing
- acceleration and deceleration
- multiple motor driving
- stop spinning after number of step, or continuos spinning mode
It would be easly portable on other microprocessor.
To rotate a motor at constant speed, pulses must be generated at a steady rate. Otherwise it must be implemented a acceleration or deceleration ramp.
Suppose the function for calculating the next pulse is called with frequency f.
The time to next pulse t, depends on the counter c.
The above image is the pulse sequence to drive a motor at constant speed or during acceleration.
The ideal ramp cure it is so draw by imposing the counter vector c, from step 0 to n step.
where the initial c0 value is calculated by the forumla:
given alpha the motor step angle, omega the motor speed and omega' the motor acceleration.
This speed ramp for a stepper motor is hard to be calculated in real-time on a low math resource microcontroller. Luckly David Austin in the paper "Generate stepper-motor speed profiles in real time" approximate that curve using Taylor series to
A further approximation proposed by the "AVR446: Linear speed control of stepper motor" Application Note by Atmel is the convertion of the above formula from float to integer math, using the remainder of the division loaded in the vector r.
I've used this approximation to implement my library. AVR446 use this method to set the timer frequency, instead i use a fixed frequency timer and then i set a counter to control when the pulse has to be emitted. In this way i can drive multiple motor with different ramp and speed.
This library use the TIMER0 to control the number of pulse to emit, other timer can be setup.
Below you can find approximation of the float and integer ramp, for acceleration and deceleration, for a counter of 100, and one of 1000, over 256 steps (n), note that the deceleration ramp for a 100 counter is really different from the acceleratin one.
An helper function is provided to compute the number of steps required to perform a shaft revolution.
This library was developed on Eclipse, built with avr-gcc on Atmega8 @ 8MHz.
Errors feedback and improvements tips are welcome.
Code
Notes
- read risk disclaimer
- excuse my bad english